船舶用距離表　Distance Table

Distance Table （距離表) の作成は、主として二等航海士の仕事です。

航海計画の基本となる航路選定においては、船長がコースラインを引く場合もありますが、
「ここと、ここと、ここを通るからね。それから、陸岸からは１５マイルぐらい離しとくように。」
なんて言って、船長はブリッジを下りていきます。だいたいその意向に添って二航士がコースラインを引くことになります。できあがると、船長にチェックしてもらいますが、大抵は修正されません。
その後ディスタンスをデバイダーで拾ったり、航法計算したりしてディスタンステーブルを完成させます。
私は22歳でセコンドになりましたので、ほとんど経験がありませんでした。それで、前任の方にひつこいぐらいに訊きました結果、一航海で２種類のディスタンステーブルを作ることにしました。それが下記しました１及び２です。対比して見て下さい。

1. Ｓｉｄｎｅｙ　～　Ｍｅｌｂｏｕｒｎｅ

陸上の道路マップなんかにもこのタイプがありますね。私は乗組員全員に配る用として作成していました。

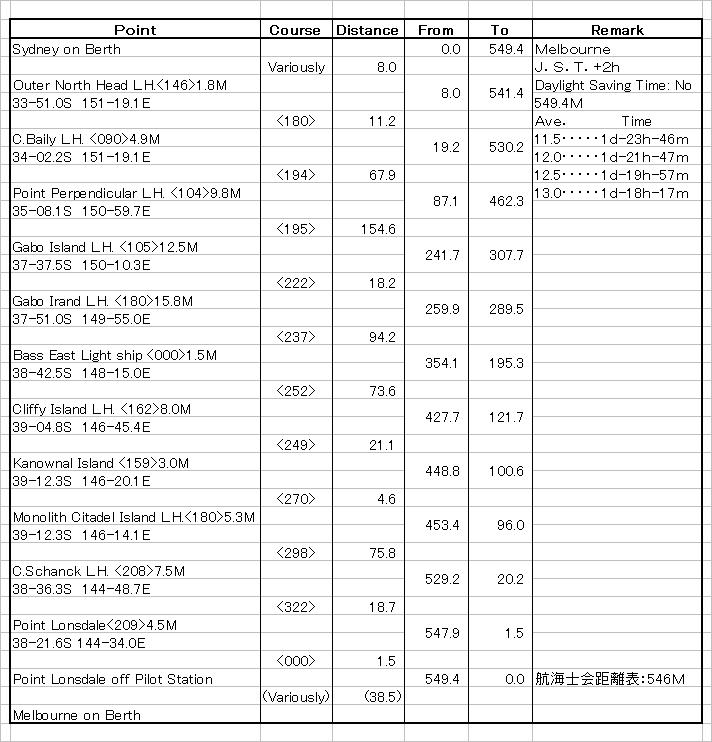
2. Sidney　～　Melbourne

このタイプは航程計算帳としてブリッジに備え置き、誰でも見れるようにしていました。

3. 横浜　～　名古屋

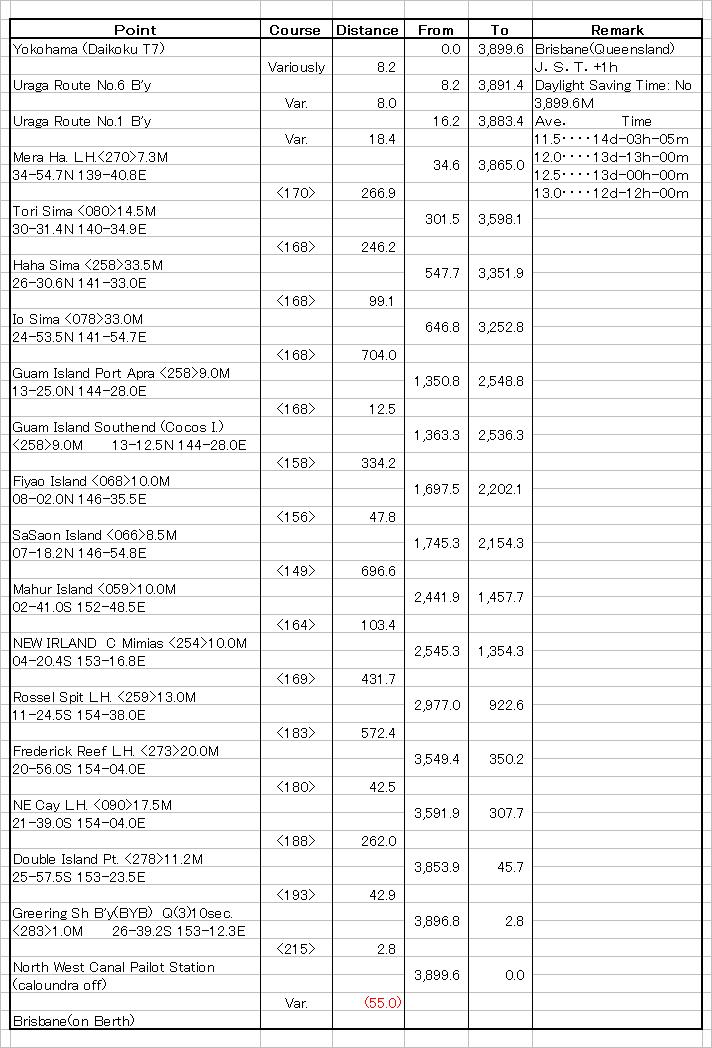
4. 横浜　～　Brisbane

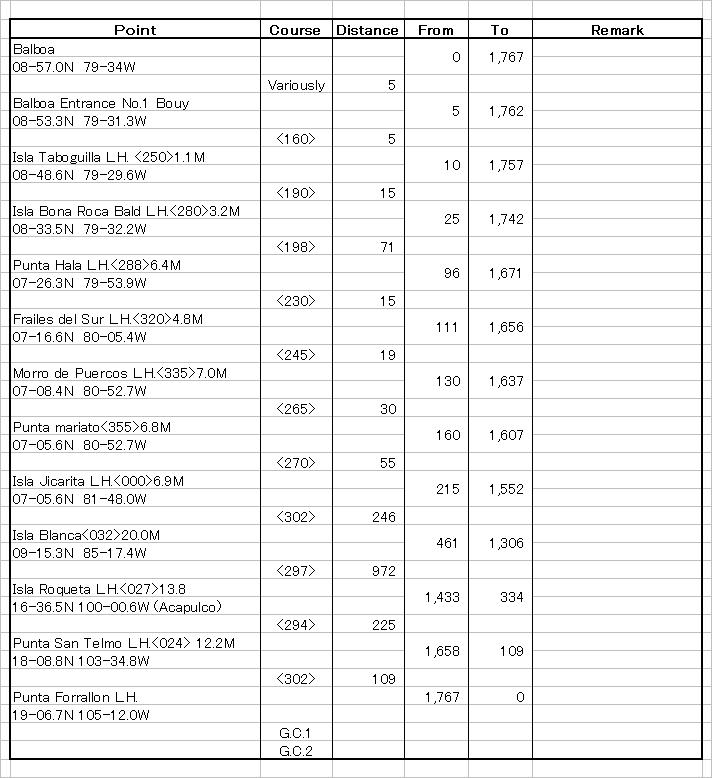
5. Balboa(Panama)　～　Yokohama

5.(1) Balboa ～ Yokohama (大圏航法）

地球の中心を通る平面で輪切りにした球面上円周を大圏と言い、その線上にある２地点間の距離は最短となります。例えば日本からロスへ行く場合は、子午線に９０°（正確にいうと少し違います）で走れば良いわけですが、それでは最短距離にならないということです。（地図上の最短距離は地球上の最短距離ではありません）結果、航海日数の短縮、延いては燃料の節約に繋がりませんので、船では大圏航路を選択して航海します。

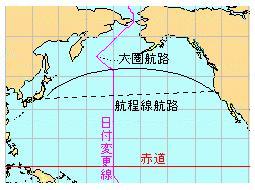　メルカトル図法では大圏航路の方が遠回りに見えます。

大圏航法のメリットは東西航行、高緯度の長距離航海で顕著ですが、南北航行、低緯度の航海や短距離では利点が少ないです。よって主に太平洋・大西洋横断等に用いられます。その針路及び距離は球面三角形の公式によって算出できますし、大圏航法図で２地点間を直線に結び、その後、決定した経度差（通常５°程度）をもって、その緯度を読み取り、漸長航法図にそれらを移し変えて求めることもできます。後者の方が楽なので一般的でしたが、現在では出発地と到着地の緯度経度を入力すれば、必要な情報が得られるような航海計器類があると思います。

それでは、大圏で航海しなかった場合には、どれほどの距離になるかを、目安として中分緯度航法を使って計算比較します。

　　　　　出発緯度　　 22゜-20.9Ｎ　　　　　　　　　　　　　　出発経度　　　110゜-00Ｗ

　　　　　到着緯度　　34゜-50.0Ｎ　　　　　　　　　　　　　　到着経度　　　140゜-00Ｅ

　　　　　変緯( D.lat) . 12゜-29.1Ｎ = 749.1　　　　　　　　　変経（D.long) 　110゜-00Ｗ = 6,600'

　　　　　Mid lat. 　　　 28゜-35.5 = 28.59

Dep.=D.long 　x　 cos Mid lat. = 6,600 x cos28.59 = 5,795.2

tan Course = Dep. / D.lat = 5,795 / 749.1 = 7.7362568

Course = tan^-1 7.7362568 = 82.6 →　Ｎ82.6Ｗ

Dist. = D.lat. x sec Course = 749.1x sec 82.6゜=　5,816'

よって、出発地から唯単にコースＮ82.6Ｗで到着地まで航海した場合には、大圏で航海した場合の 5,566' （上記表参照 5,614' - 48' = 5,566）より、250' も長くなってしまいます。

5.(2) Balboa ～ Yokohama (集成大圏航法）

集成大圏航法とは大圏航法のうち、障害物や気象などの影響を考慮してある区間のみ大圏航路を離れて航海するものです。例えば、高緯度を航行しますと、季節によっては荒天が予想され、航走距離が短いからと無理をして大圏を航行しても危険ですし、期待する成果は上がりません。従って、その区域を避けるため制限緯度を設けて、東西に航行します。そして、その航程線が元の大圏航路と交わったところで再び大圏航法に復帰させます。
以下の表では北緯４０゜を上限緯度として、集成大圏航法をとりました。

ディスタンステーブルの例をいくつか記します。

1.	Sidney ～ Melbourne 1

2.	Sidney ～ Melbourne 2

3.	横浜　～　名古屋

4.	Yokohama ～ Brisbane

5.	Balboa(Panama) ～ Yokohama
	(1)大圏航法 (Great-Circle Route)
	(2)集成大圏航法 (G.C.R. & Rhumb Line)

	作者著書